离散特征
何为离散特征?
性别:男、女
国籍:中国、美国…
英文单词:常见的英文单词有几万个
物品ID:小红书有几亿篇笔记,每篇笔记都有一个ID
用户ID:小红书有几亿个用户,每个用户有一个ID
离散特征的处理
- 建立字典:把类别映射成序号
- 中国->1
- 美国->2
- 澳洲->3
- 向量化:把序号映射成向量
- One-hot编码:把序号映射成高维稀疏向量
- Embedding:把序号映射成低维稠密向量
One-hot是怎么做的
比如用200维稀疏向量表示国籍
- 未知->0->[0,0,0,…,0]
- 中国->1->[1,0,0,…,0]
- 美国->2->[0,1,0,…,0]
One-hot的局限
对于性别这样的特征用One-hot还算可以,但是对于很多其他场景就不合适了,自然语言处理中,对单词做编码,英文有几万个单词,那么One-hot向量的维度是几万;推荐系统中,对物品ID做编码,小红书有几亿篇笔记,那么One-hot向量的维度是几亿。
Embedding是怎么做的
参数数量:向量维度*类别数量
- 设Embedding得到的向量都是4维的
- 一共有200个国籍
- 参数数量=4*200=800
编程实现:TensorFlow、Pytorch提供的embedding层
- 参数以矩阵形式保存,矩阵大小也就是参数数量
- 输入是序号,比如美国的序号是2
- 输出是向量,比如美国对应参数矩阵的第2列
Embedding其实就是参数矩阵乘One-hot向量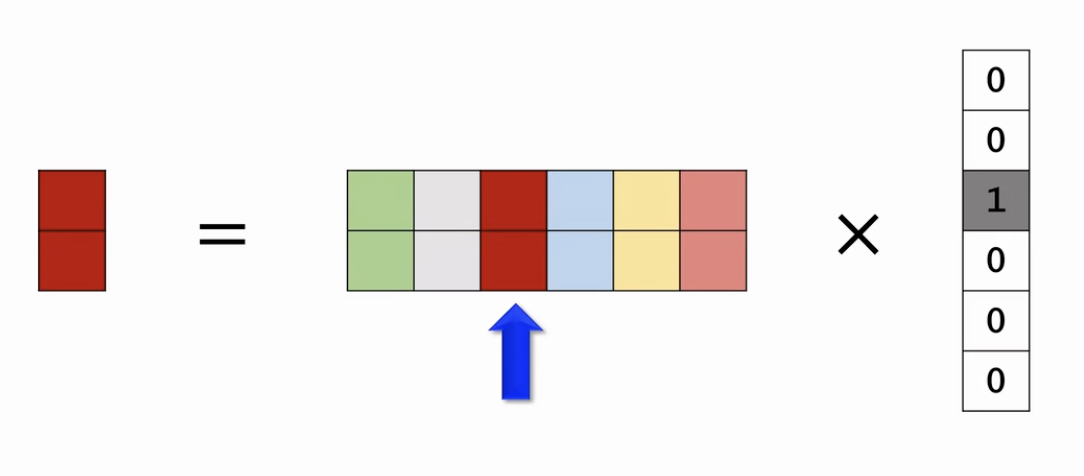
矩阵补充
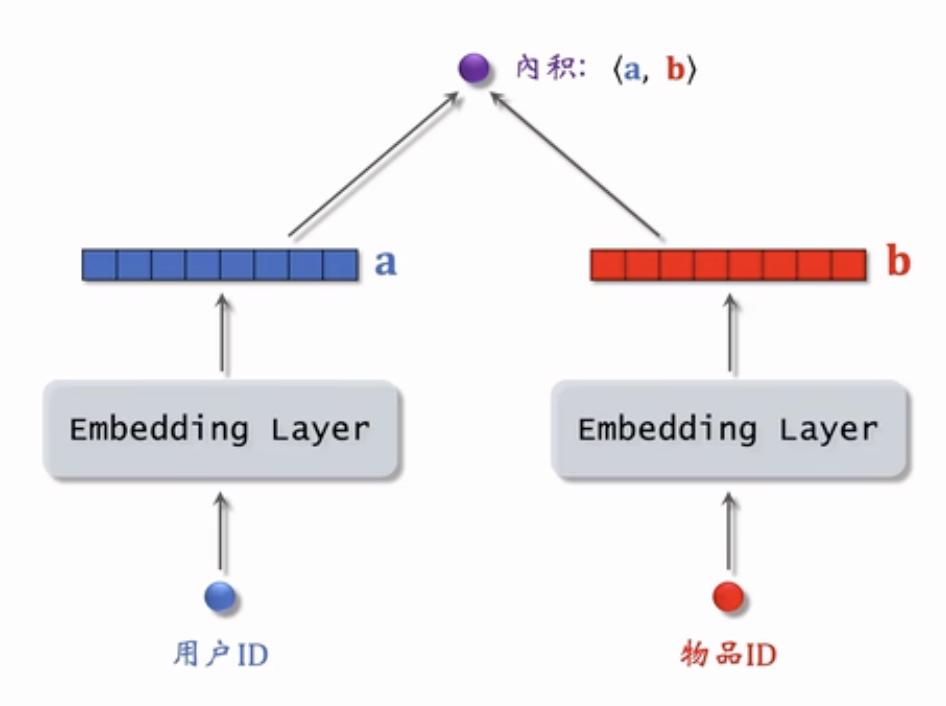
上图a和b分别是用户ID和物品ID的Embedding层输出的某一列,每一列代表一个用户或者物品,两个Embedding层不共享参数,a和b向量做内积得到a用户对b物品预估的偏好得分,模型训练的目的就是学习矩阵A和B,使得预估值拟合真是观测的兴趣分数
把用户 ID、物品 ID 映射成向量:
- 第 $u$ 号用户 $\rightarrow$ 向量 $\mathbf{a}_u$
- 第 $i$ 号物品 $\rightarrow$ 向量 $\mathbf{b}_i$
求解优化问题,得到参数 $\mathbf{A}$ 和 $\mathbf{B}$:
$$
\min_{\mathbf{A}, \mathbf{B}} \sum_{(u, i, y) \in \Omega} \left( y - \langle \mathbf{a}_u, \mathbf{b}_i \rangle \right)^2
$$
其中:
- $\Omega$ 表示训练集中已观察的评分集合;
- $\langle \mathbf{a}_u, \mathbf{b}_i \rangle$ 表示用户与物品向量的内积;
- $y$ 是用户 $u$ 对物品 $i$ 的真实评分。
矩阵补充在实践中效果不好
- 缺点1:仅用ID embedding,没有利用物品、用户属性
- 缺点2:负样本的选取方式不对,样本为用户-物品二元组,记作(u,i),正样本的选择是正确的,曝光之后,有点击、交互就算正样本;但是负样本的选择为曝光之后,没有点击、交互,这是错误的,因为虽然有一部分是系统认为用户喜欢的,但用户确实不喜欢,这一部分是真正的负样本,但还有一部分可能是用户可能感兴趣但没看到,这些不是真正的负样本,把它们强行标记为负样本,会误导模型
- 缺点3:做训练的方法不好,内积不如余弦相似度;并且用平方损失(回归)也不如用交叉熵损失(分类)
模型存储
- 训练得到矩阵A和B,A的每一列对应一个用户,B的每一列对应一个物品
- 对于矩阵A,可以把A的列存储到key-value表,key是用户ID,value是A的一列
线上服务
把用户ID作为key,查询key-value表,得到该用户的向量,记作a
最近邻查找:查找用户最有可能感兴趣的k个物品,作为召回结果
- 第i号物品的embedding向量记作$b_i$
- 内积$<a,b_i>$是用户对第i号物品兴趣的预估
- 返回内积最大的k个物品
如果枚举所有物品,时间复杂度正比于物品数量
如何加速最近邻查找
近似最近邻查找 Approximate Nearest Neighbor Search
支持最近邻查找的系统:Milvus、Faiss、HnswLib
衡量最近邻的标准:
- 欧式距离最小(L2距离)
- 向量内积最大(内积相似度)
- 向量夹角余弦最大(cosine相似度)
加速最近邻查找的方法
划分扇形图,按照最近邻衡量标准不同的划分方法,划分为n个区域,每个区域用一个向量代表这个区域,将n个代表向量为key,每个区域中的点为value。
这样就可以快速做线上召回了,只用将某个用户embedding和每个物品代表向量做相似度计算,以找到最相似的代表向量,也就找到了里面的value,再对这个区域里所有的点做相似度计算,大大减小了计算次数
线上召回
把用户向量a作为query,查找使得$<a,b_i>$最大化的物品i
暴力枚举速度太慢,实践中用近似最近邻查找
工业界会用一些开源的向量数据库Milvus、Faiss、HnswLib,支持最近邻查找
双塔模型
矩阵补充模型的升级版,矩阵补充只用到了用户和物品的ID,比较弱,没有用到两者分别的属性
下图为得到用户表征向量和物品表征向量就可以做余弦相似度计算相似度score
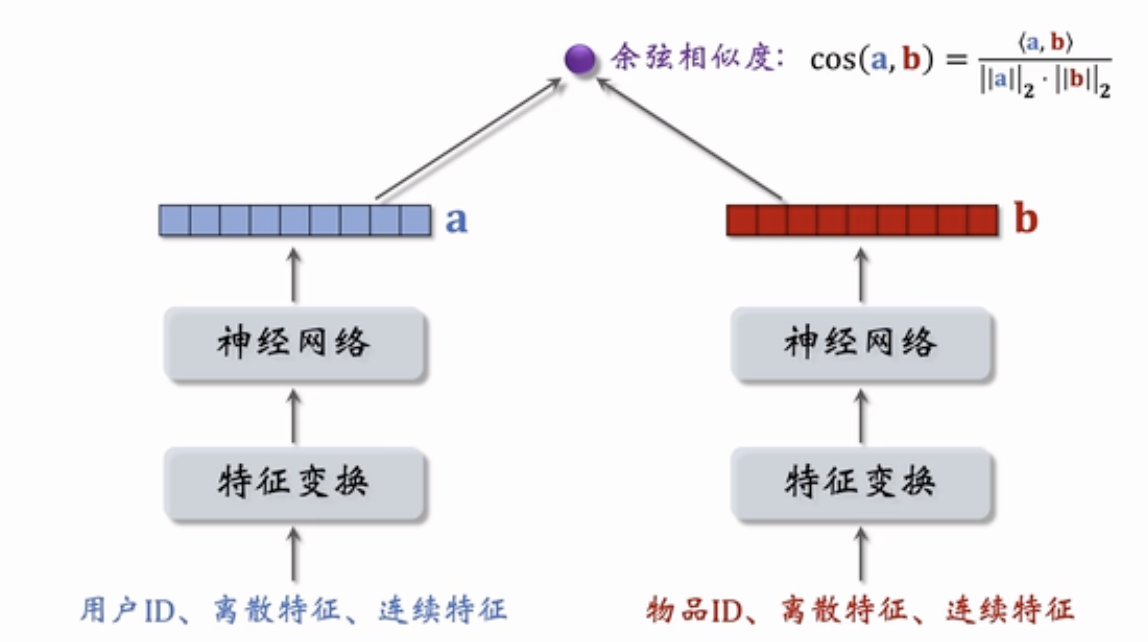
用户属性
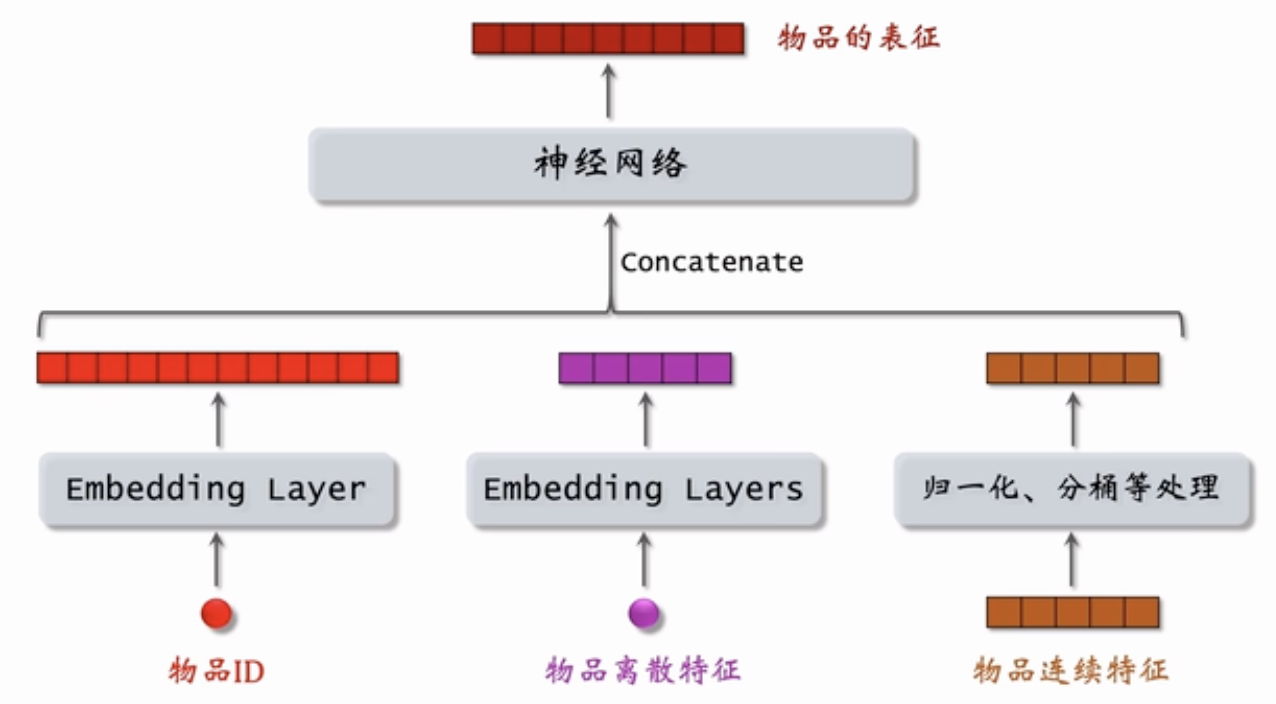
用户ID,同矩阵补充模型,使用一个Embedding Layer
用户离散特征,每个特征使用一个Embedding Layer,有n个离散特征(如果特征值比较少,比如性别这样的,可以用one-hot)
用户连续特征,归一化、分桶等处理
拼接起来输送到神经网络,输出用户的表征
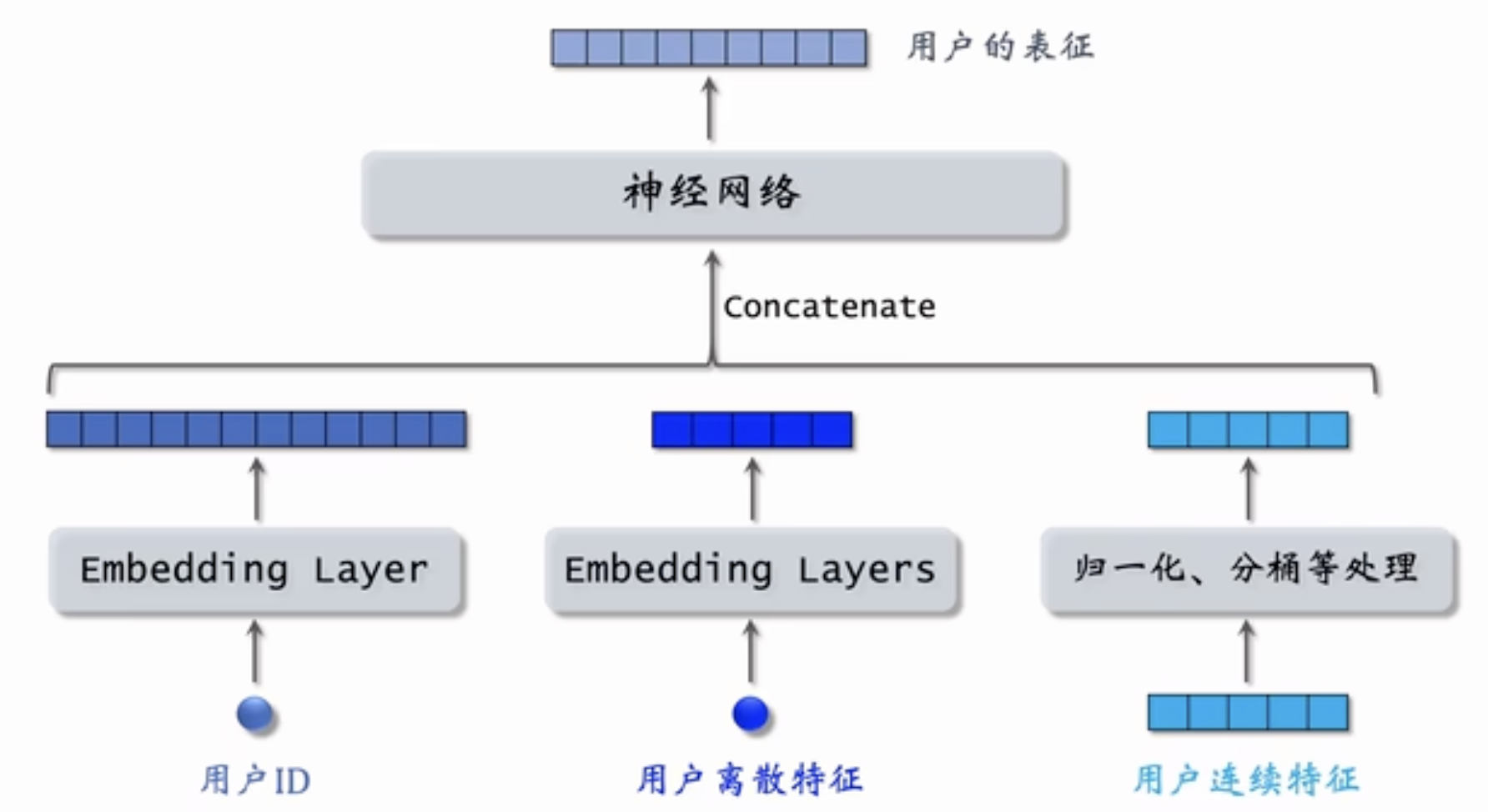
物品属性
同用户属性,得到物品的表征
训练
- Pointwise:独立看待每个正样本、负样本,做简单的二元分类
- Pairwise:每次取一个正样本、一个负样本
- Listwise:每次取一个正样本、多个负样本
正负样本的选择
正样本:用户点击的物品
负样本:
- 没有被召回的?
- 召回但是被粗排、精排淘汰的?
- 曝光但是没有被点击的?
Pointwise
好处:召回阶段的目标是判断用户-物品对的“相关性”(如点击/未点击),本质是二分类问题(正样本=用户感兴趣,负样本=不感兴趣)。
对于正样本,鼓励$cos(a,b)$接近1,
对于负样本,鼓励$cos(a,b)$接近-1。
控制正负样本的数量为1:2或者1:3,为什么?
解决数据不平衡问题
真实场景中,正样本(点击/交互)远少于负样本(比如说未点击),若负样本过多,模型会偏向预测为负(准确率虽高但召回率低),1:2 或 1:3 的比例 是对负样本的降采样,平衡类别分布,避免模型偏见。
Pointwise 简单高效,适合大规模召回
在召回阶段,快速筛选候选集比精确排序更重要,因此 Pointwise 更常用。
Pairwise
物品不管正负样本,神经网络中的参数共享
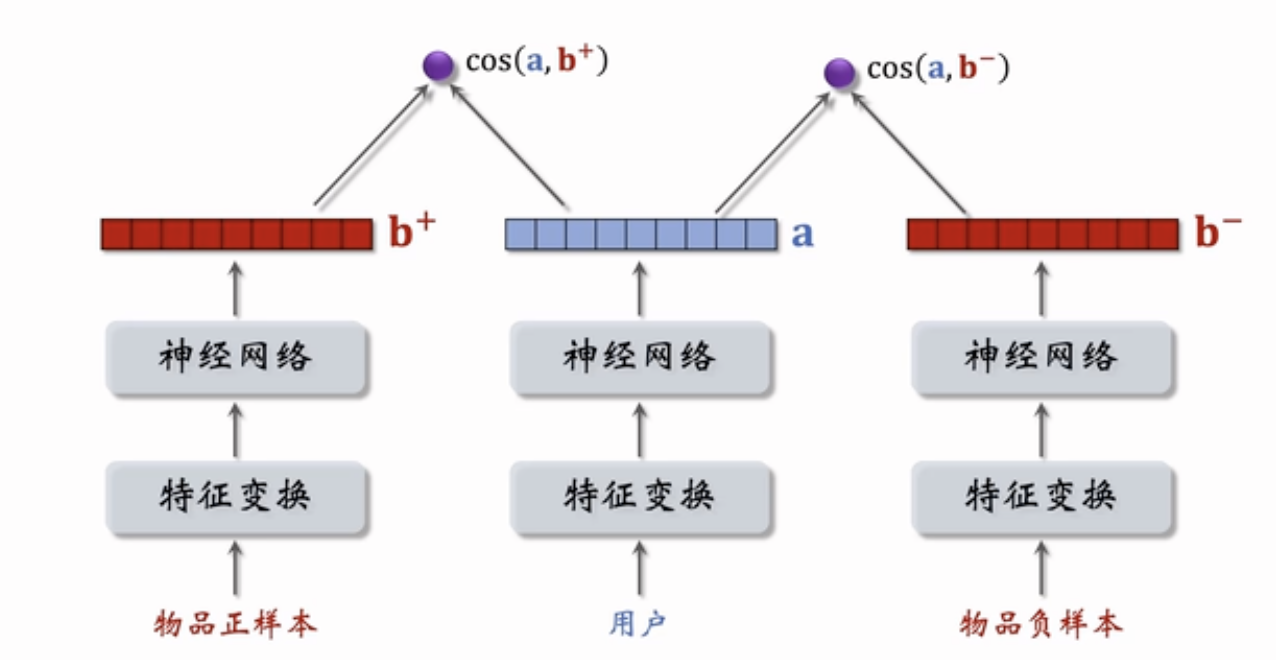
鼓励$cos(a,b^+)$大于$cos(a,b^-)$
- 如果$cos(a,b^+)$大于$cos(a,b^-)+m$,则没有损失,其中m是一个超参数
- 否则,损失等于$cos(a,b^-)+m-cos(a,b^+)$,那就说明有损失
可以推出Triplet hinge loss
$$
L(a,b^+,b^-)=max\{0,cos(a,b^-)+m-cos(a,b^+)\}
$$
Triplet logistic loss
$$
L(a,b^+,b^-)=log(1+exp[\sigma.(cos(a,b^-)-cos(a,b^+))])
$$
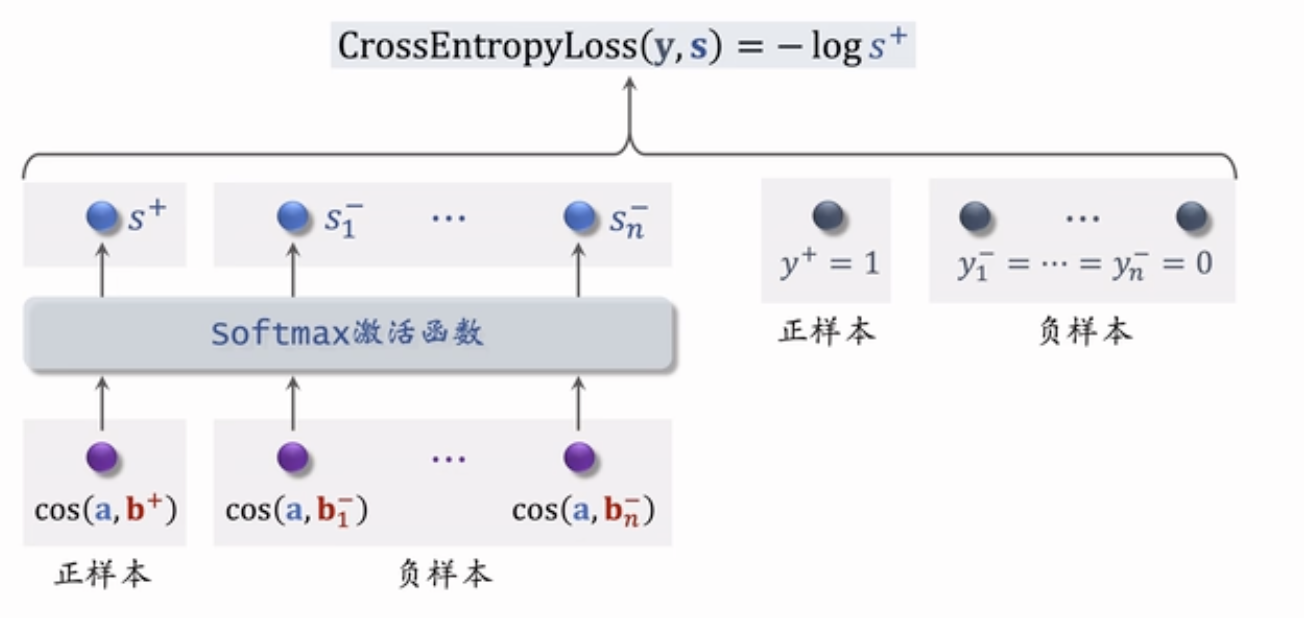
Listwise
一条数据包含:
- 一个用户,特征向量记作a
- 一个正样本,特征向量记作$b^+$
- 多个负样本,特征向量记作$b_1^-,…,b_n^-$
鼓励$cos(a,b^+)$尽量大
鼓励$cos(a,b_1^-),…,cos(a,b_n^-)$尽量小
前期融合or后期融合
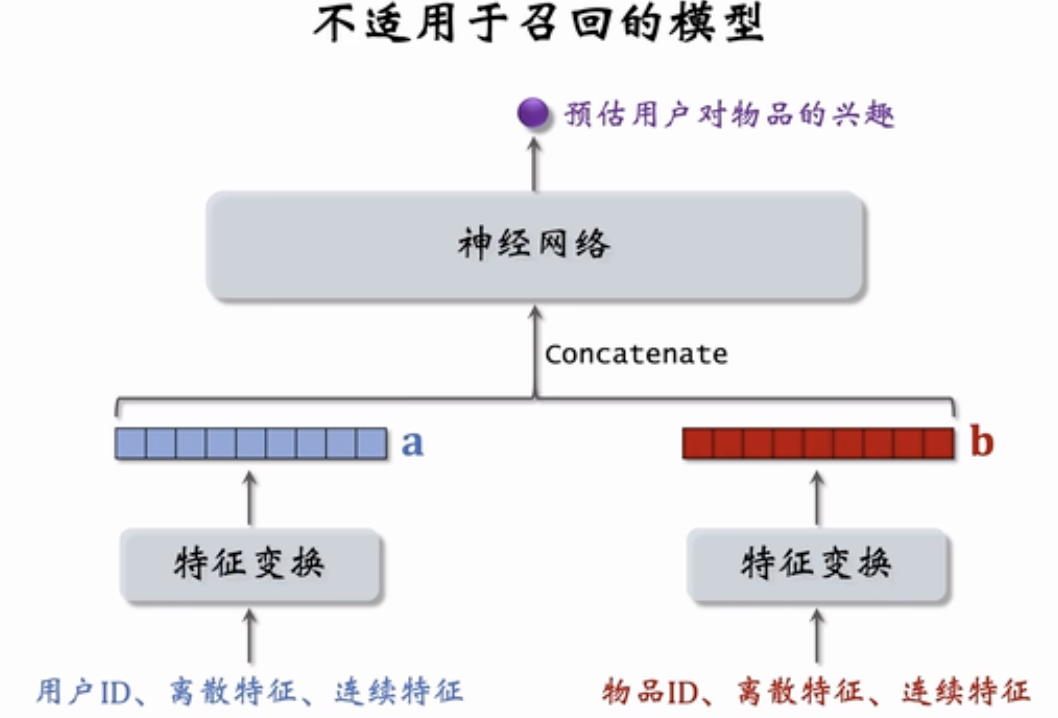
该图展示的是一种前期融合模型,将用户和物品的特征(如 ID、离散特征、连续特征)分别处理后concatenate输入到一个神经网络中预测用户对物品的兴趣。
这种结构常用于 CTR 预估,但并不适用于召回阶段。
双塔模型适合召回阶段的原因
双塔模型将用户和物品的特征分别通过神经网络编码为独立向量(Embedding),分别记作 u 和 v,用点积或余弦相似度计算两者之间的匹配度 score = dot(u, v)。
优点在于可以提前离线计算物品向量,只需在线计算用户向量后检索相似物品(如用 Faiss)。
适合大规模召回,在大规模候选集中(百万级、亿级物品),提前建好物品向量索引,用户进来后快速检索相似物品,效率高。
后期融合?
后期融合指的是:用户向量、物品向量先各自独立学习和生成,最后在推理阶段进行后期的相似度计算或打分。
在训练阶段可以使用点积 + Sigmoid 或 Softmax loss,优化匹配概率。
后期融合的特点是:结构上是解耦的,可扩展的,可缓存的,完全适合召回。
前期融合不适用于召回阶段的原因
用户和物品强耦合,无法分开计算,因为模型结构上将用户特征和物品特征拼接在一起输入神经网络,无法事先计算用户或物品的独立向量,每次都要组合后重新计算——不能提前离线建立索引。
无法实现向量检索,输出不是标准向量对之间的相似度,而是神经网络回归结果,缺乏对称性与嵌入空间的结构化表达,不适用于 Faiss 等库
设计本质是“打分”不是“召回”,适用于排序阶段的小规模候选集打分,不适合百亿级候选池的粗筛。
使用建议
双塔模型用于召回(粗排);
前期融合或深度交叉模型(如DIN、DeepFM)用于排序阶段。这样才能兼顾召回效率与排序精度。